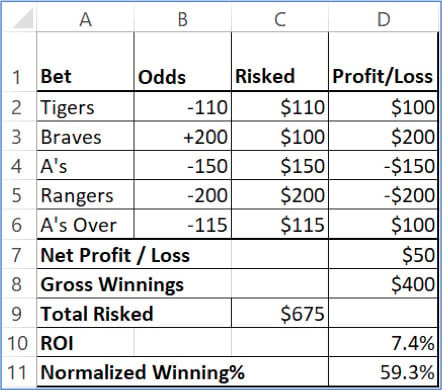
Bet Calculation Example
The effective rate of interest on the loan (as with almost on any other financial instrument) – this is the expression of all future cash payments (incomes from a financial instrument), which are included in the treaty provision of the contract, in the figure annual interest. That is the real interest that the debtor will pay for using of money in the Bank (investor – to obtain). Here is taken into account the rate of interest designated in the contract, all fees, repayment schemes, loan term (of deposit).
- Bet Surface Area Calculation Example
- Bet Surface Area Calculation Example
- Beta Calculation Examples
- Bet Calculator Example Value
- How To Use Bet Calculator
- Bet Calculator Example Definition
- Bet Calculator Example Math
Bet Surface Area Calculation Example
The calculation of the effective rate on the loan in Excel
For example, a $100 bet at -200 in American odds (1/2 in fractional or 1.50 in decimal) with a 66.67 percent implied probability has the potential to profit $50 should it win (not total return. If you bet $100, you get $120: your $100 stake + $20 profit. Below, the calculation is similar to, but not the same as, the American odds equation. Profit = (Stake x Odds) – Stake. Profit = (Stake x Odds) – Stake. So, using $100 as the stake and the example above, that would look like: Profit = (100 x 1.2) – 100 = (120) – 100 = 20.
There are the range of built-in functions in Excel, that allow you to compute the effective rate of interest, with taking into account additional charges and fees, and excluding (relying only on the nominal interest and the loan term).
The debtor took a credit in the sum of 150 000$ on the term of 1 year (12 months). The nominal annual rate - is 18%. Payments on the loan specify in the table below:
Since this example does not include the additional fees and charges, we determine to the annual effective rate using the function EFFECT.
We are calling: «FORMULAS»-«Function Library»-«Financial» finding the function EFFECT. The arguments:
- «Nominal rate» - is the annual rate of interest on the credit, which is designated in the agreement with the Bank. In this example – is 18% (0, 18).
- «Number of periods» - the number of periods in a year, for which interests are charged. In this example – there are 12 months.
The effective interest on rate - is 19. 56%.
Let's complicate the task by adding the one-time commission loan at the amount of 1% of the sum of 150 000$. In monetary terms – is 1500$. So, the borrower to get on his hands is the sum of 148 500$.
For calculating to the effective monthly rate, we need use the IRR function (return to the internal rate of return for cash flow):
We have made the column with monthly payments 148 500 with the sign «-», because the money the Bank first gives. Payments which the debtor will make in the cashier subsequently are positive for the bank. The internal rate of return we consider from the Bank's point of view: it acts as an investor.
The function has given to the effective monthly rate of 1.6617121%. For the calculating of the nominal rate to the result need multiply by 12 (the term of loan): 1.662% * 12 = 19.94%. Let`s recalculate the effective interest percent:
The one-time fee in amount of 1% increased the actual annual interest on 2.31%. It was: 21, 87%.
We add in the scheme of payments on the loan to the monthly fee for account maintenance in the amount of 30$. Monthly effective rate will be equal to 1.6968%.
The nominal percent is 1.6968% * 12 = is 20.3616%. The effective annual rate is:
The monthly fees increased till 22, 37%. But in the loan contract will continue to be the figure of 18%. However, the new law requires banks to specify in the loan agreement to the effective annual interest rate. However, the borrower will see this figure after the approval and signing of the contract.
What distinguishes a lease from a loan
Leasing – this is the long-term rental of vehicles, real estate, equipment, with the possibility of their future redemption. The lessor acquires to the property and transfers it under the contract to a physical / legal person under certain conditions. The lessee uses to the property (in personal/ business purposes) and pays to the lessor for the right of using.
In the essen, it`s the same loan, only to the property will belong to the lessor until the lessee is fully repaid to the asset purchased plus interest.
The computation of the effective percent on leasing in Excel is followed on the same scheme as the computation of the annual interest rate on the credit. There is the example with another function.
The data input:
Bet Surface Area Calculation Example
You can go on already blazed way: to computation the internal rate of return, and then multiply the result by 12. But we using the function =XIRR(it returns to the internal percent of return for the schedule of cash flows).
The function arguments:
Beta Calculation Examples
The effective interest on the lease was % to 23. 28%.
Bet Calculator Example Value
Calculation of the effective interest rate on OVDP in Excel
How To Use Bet Calculator
OVDP - domestic government loan bonds. They can be compared with the deposits in a bank. So how exactly the investor gets to a refund of the full amount of invested funds plus additional income as a percentage. The guarantor of the safety of funds is the National Bank.
The effective interest allows estimate to the real income, because it takes into account to capitalization of interest. For example, «acquire» one-year bonds in the sum of 50 000 at 17%. To calculate your income, using the function =FV():
Bet Calculator Example Definition
Suppose that the interest to capitalize by monthly. Therefore, we divide 17% by 12. The result as a decimal insertion we put in the field «Bet». In the «Nper» we enter to the number of periods of compounding. Monthly fixed payments we will not get, so the field «Pmt» leaving free. In the column «Pv» we put the deposit invested funds with the sign «-».
Bet Calculator Example Math
In the window, we immediately see to the sum, which you can get for the bonds in the end of the term. This is the monetary value of accrued compound interest.